Magical Power of Quantum Mechanics

QM Magic Class | Chapter 19

Chapter 7, left us with a surprising observation reported by McDonald et al. in 2006 ^[1]: 2,3-dichloro-pyrazine reacts with lithium dithiane to provide a single product in which the hydrogen atom at C-6 of pyrazine is substituted by the nucleophile and the chloro group at C-3 is replaced by a hydrogen atom. In contrast to the selective C-2 chloride displacement usually observed for reactions between 2,3-dichloropyrazine and other nucleophiles (e.g. amines, enolate anions, etc.) (Figure 1). ^[2]

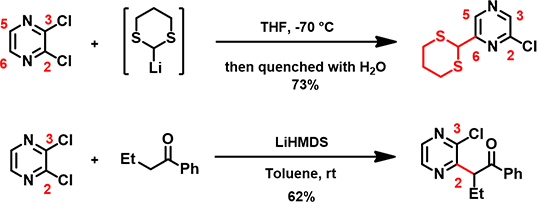
Figure 1. Nucleophilic Substitution of 2, 3-Dichloropyrazine at C2 and C6

Why does lithiated dithiane add to 2,3-dichloropyrazine at C-6 position? Why would the chloro group at C-3 be selectively displaced?

LUMO & LUMO Map Analyses

Since 2,3-dichloropyrazine is the electrophile in the reaction, let’s look at its LUMO and LUMO Map first (Figure 2). This dichloropyrazine has its LUMO lobes centered mainly between C-2 and C-3, C-5 and C-6 (colored in red), not on the carbons themselves, while LUMO + 1, 0.65 eV higher in energy than LUMO, has significant lobes centered on C-2, C-3, C-5 & C-6, and are roughly equal in sizes.

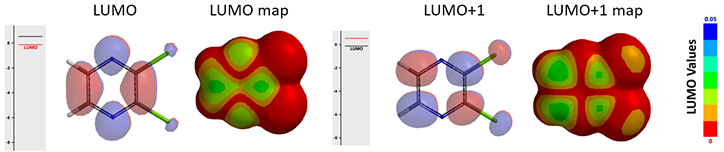
Figure 2. LUMO/LUMO map (left) and LUMO + 1/LUMO + 1 map (right) of 2,3-dichloropyrazine

LUMO + 1 map reveals that the LUMO+1 lobes on C-5 and C-6 are more exposed beyond the surface of the molecule than the lobes on C-2 and C-3 (due to the attached chloro groups), and LUMO ones, suggesting a higher accessibility for nucleophilic attack at C-5 and C-6. It is more likely that 2,3-dichloropyrazine uses LUMO+1 for the addition.

Reversibility and Irreversibility of Interactions

Based on the LUMO + 1/LUMO + 1 map analyses, we reason that C-6 of 2,3-dichloropyrazine is more accessible than C-2 for nucleophilic interaction with lithium enolate (Figure 3). However, such reaction at the C-6 is reversible, while addition at the C-2 position could lead to displacement of the chloro group, an irreversible process.

Figure 3. Nucleophilic substitution of 2, 3-dichloropyrazine with lithium enolate

When lithiated dithiane is used in the reaction (Figure 4), since C-6 is more accessible than C-2 and formation of this carbon-carbon bond is irreversible, preferential addition of dithiane occurs at the C-6.

Figure 4. Nucleophilic Substitution of 2,3-dichloropyrazine with lithiated dithiane

Next question, why is the chloro group at C-3 being selectively displaced?

Mechanism for Chloride Elimination

We propose the reaction mechanism shown in Figure 5. First, 2,3-dichloropyrazine reacts with lithiated dithiane irreversibly to provide intermediate I (along with its resonant structures I’ and I”); after quenching with water, the anionic intermediate acquires a proton to form compound B, which potentially is an equilibrium mixture of B1, B2, B3 and B4 ; Intermediate B eliminates a molecule of HCl, re-aromatizes to provide product C, analogous to the mechanism proposed by McDonald et al for 2,6-dichloropyrazine tele-substitution. ^[1]

Figure 5. Proposed mechanism: Reaction of 2,3-dichloropyrazine with lithiated dithiane

Next question becomes “Elimination of HCl proceeds via B1, B2, B3 or B4?” Density Functional Theory equilibrium geometry calculations (polar solvent) suggests an equilibrium distribution in the ratio of 0.0 : 0.8 : 7.2 : 91.9% for B1, B2, B3 and B4, respectively (Figure 6). B1 has the highest energy and its distribution is almost zero. Isomer B4 has the lowest energy of -6.53 kcal/mol and the highest distribution percentage, presumably due to stabilization from the conjugated N=C-C=N system. But since both of its chloro groups are attached to sp2 hybridized carbon atoms, they are not amendable to undergo HCl elimination. B2 and B3, with their C=N bonds not in conjugation, are higher in energy than B4. How could we evaluate them for subsequent elimination?

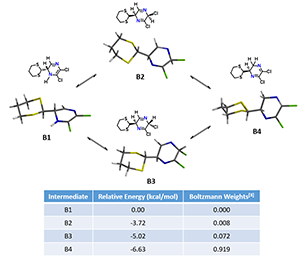
Figure 6. The four possible structures of B, their relative energies and distribution.

Reaction Energy Profile Calculation

When water is added to quench the reaction, hydroxide is generated. Shown on Figure 7 is the reaction energy profile we modeled for B-3 HCl elimination with hydroxide. The C-H bond distance at C-6 increased from 1.096 to 3.096 Å with a step size of 0.2 Å. Modeling result suggests a concerted departure of the pseudo-axial proton at C-6 and the pseudo-axial chloro group at C-3, and the chloride interacts with the water molecule formed. C-3 and C-6 change from sp3 to sp2 hybridization, and the molecule aromatizes to provide compound C. Calculation also indicates that this elimination has no activation energy barrier to overcome, and should be a very fast process.

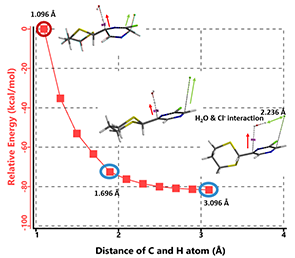
Figure 7. Modeling of B3 HCl elimination with hydroxide anion

For intermediate B2, with the departing chloro in pseudo-equatorial position (Figure 8), reaction energy profile calculation does not arrive at elimination product and suggests a high activation barrier, making this pathway not likely.

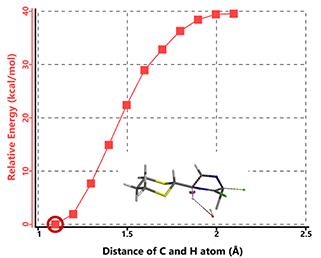
Figure 8. Modeling of B2 HCl elimination with hydroxide anion

In summary, LUMO/LUMO map analyses of 2,3-dichloropyrazine, irreversible nature of lithiated dithiane addition, and reaction energy profile calculation of the HCl elimination step, provide us with satisfactory explanations to the “surprising” tele-substitution product observed by McDonald et al.

Building on What We Just Learned

In the same paper, McDonald et al also reported that treatment of 2,6-dichloropyrazine with lithiated dithiane led to another tele-substitution product.

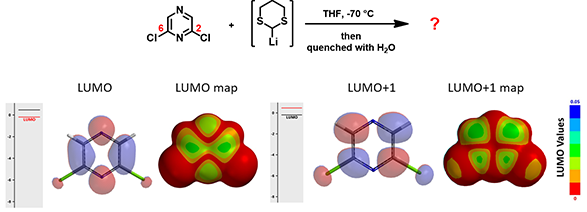
Figure 9. LUMO/LUMO+1 and LUMO/LUMO+1 map of 2,6-dichloropyrazine

Shown in Figure 9 are LUMO/LUMO + 1 and LUMO/LUMO + 1 map of 2,6-dichloropyrazine. How will the addition and elimination proceed? What could be the structure of the product identified?

 
 
References:
 
[1] Torr, J.E., Large, J.M., Horton, P.N., Hursthouse, M. B., McDonald, E. Tetrahedron Lett. 2006, 47, 31.
 
[2] J. A. Joule & K. Mills. Heterocyclic Chemistry 5th Ed. Chichester, West Sussex, UK: Blackwell Publishing Ltd., 2010. Pg. 256-7.
 
[3] Boltzmann Weights: Distribution of equilibrating isomers at thermodynamic equilibrium, based on difference in their energies.
 
This article is written and edited by Liting Dong, Zhengquan Zhou, Tommy Lai, Dong Pan, Guqin Shi, Yongsheng Chen, and John S. Wai.